Các bạn học sinh đang tìm hiểu về số chính phương, kiến thức quan trọng trong chương trình Toán học. Học Toán không đơn giản khi người học cần sự tư duy, suy luận logic để hiểu hơn về các con số và những bài toán. Trong kiến thức lần này, chúng tôi xin giới thiệu với các bạn về số chính phương là gì? Tính chất và đặc điểm số chính phương. Mời các bạn học sinh cùng theo dõi bên dưới.
Contents
Số chính phương là gì?

Số chính phương hay số hình vuông là số tự nhiên có căn bậc 2 của số tự nhiên. Nói một cách dễ hiểu hơn số chính phương là lũy thừa bậc 2 của 1 số tự nhiên nào đó.
Số chính phương có đặc điểm là số không âm. Hay số chính phương có căn bậc hai là một số nguyên.
Nhận biết số chính phương thế nào?
Dựa trên khái niệm về số chính phương bên trên. Bạn có thể tìm ra dấu hiệu nhận biết. Sau đây là các dấu hiệu cơ bản về số chính phương.
– Dựa vào hàng đơn vị: hàng đơn vị của số chính phương 0, 1, 4, 5, 6, 9. Trong trường hợp hàng đơn vị là các con số còn lại có nghĩa không phải là số chính phương.
– Căn cứ vào đặc điểm về số chính phương.
Đặc điểm số chính phương
Số chính phương có các đặc điểm cơ bản như sau:
– Phân tích một số chính phương ra thừa số nguyên tố thu được thừa số là lũy thừa của số nguyên tố với số mũ chẵn.
– Số chính phương hàng đơn vị không bao giờ là 2, 3, 7, 8, như vậy số chính phương có chữ số tận cùng là 0, 1, 4, 5, 6, 9.
– Số chính phương chia cho 3 không dư 2, số chính phương chia cho 4 không dư 2 hoặc 3, số chính phương lẻ khi trường hợp chia 8 dư 1.
– Công thức tính hiệu hai số chính phương: a2-b2=(a+b)(a-b).
– Số ước nguyên dương của số chính phương là số lẻ.
– Tổng số chính phương viết thành dãy tổng các số lẻ tăng dần theo thứ tự như sau 1: 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, 1 + 3 + 5 + 7 + 9…
Các dạng số chính phương
Số chính phương ở các dạng cơ bản sau đây:
Dạng 4n. Không có số chính phương dạng 4n + 2
Dạng 4n + 1. Không có số chính phương dạng 4n + 3
Dạng 3n. Không có số chính phương dạng 3n + 2
Dạng 3n + 1. Không có số chính phương 3n + 2
Chứng minh số chính phương
Thông thường học sinh sẽ thực hành bài toán chứng minh n là số chính phương hoặc chứng minh n không phải là số chính phương.
Chứng minh N là một số chính phương:
– Biến đổi N thành bình phương 1 số tự nhiên.
– Áp dụng tính chất: nếu 2 số tự nhiên a và b nguyên tố cùng nhau có tích là số chính phương thì a và b là các số chính phương.
Chứng minh N không phải một số chính phương:
– Chứng minh N ở hàng đơn vị hoặc tận cùng 2 3 7 8 hoặc N tận cùng là 2k + 1 chữ số 0.
– Chứng minh N chứa số nguyên tố có số mũ lẻ.
– Xem số dư, khi dùng N chia cho các số là 3 hoặc 4, 5, 8 ,…Ví dụ số N chia 3 dư 2 hoặc chia 4 dư 2 => số N không phải là số chính phương.
– Chứng minh số N nằm ở vị trí giữa hai số chính phương liên tiếp.
Ví dụ số chính phương
Từ đặc điểm của số chính phương, học sinh dễ dàng đưa ra các ví dụ minh họa về số này. Dưới đây là các ví dụ tham khảo về số chính phương dành cho các bạn chưa biết.
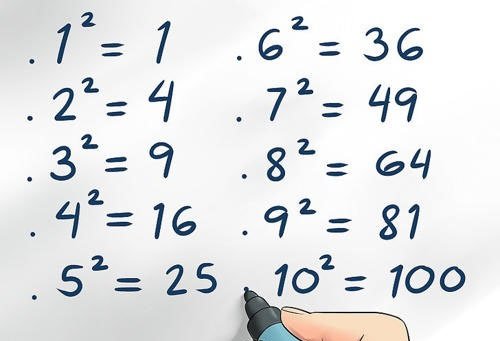
Ví dụ:
4 là một số chính phương. Vì 2 bình phương sẽ bằng số 4.
324 là một số chính phương vì 18 bình phương bằng 324.
9 là một số chính phương vì 3 bình phương bằng số 9.
1.000.000 là số chính phương bởi 1000 bình phương bằng 1.000.000.
Xem thêm: Cách học tốt môn toán hiệu quả nhất
Như vậy các bạn đã hiểu được số chính phương là gì đúng không nào? Đặc điểm cùng với một số ví dụ cơ bản về số chính phương cực kỳ dễ hiểu dành cho học sinh. Nhận biết số chính phương giúp học sinh hiểu bài và giải bài tập hiệu quả hơn.