Cách xác định tâm đường tròn nội tiếp tam giác

Tâm đường tròn nội tiếp là một khái niệm trong toán học liên quan đến các đường tròn trong một tam giác. Nó là một đường tròn nằm trong tam giác và cắt đều ba đường thẳng của tam giác. Tâm đường tròn nội tiếp cũng là trung điểm của tam giác và đặt tại giữa hai cạnh của tam giác. Nó cũng có thể được xác định bằng các công thức toán học.

Cho tam giác abc nội tiếp đường tròn tâm o

Với tam giác ABC và tâm đường tròn nội tiếp là O, chúng ta có thể biết:

1. O là trung điểm của tam giác ABC.
2. Các đoạn thẳng BO, CO, và AO là cắt đều ba cạnh của tam giác ABC.
3. AB, BC, và AC là đỉnh của tam giác ABC và là cạnh của tam giác.
4. Đoạn thẳng OA, OB, và OC là trung tâm của các cạnh của tam giác.
5. Khi AO gặp BO, O là trung điểm của AB.
6. Khi BO gặp CO, O là trung điểm của BC.
7. Khi CO gặp AO, O là trung điểm của AC.

Như vậy, tâm đường tròn nội tiếp là một khái niệm quan trọng trong toán học và có rất nhiều ứng dụng trong thiết kế, xây dựng, và các lĩnh vực liên quan.

Tâm đường tròn nội tiếp tam giác là

Tâm đường tròn nội tiếp là một đường tròn nằm trong tam giác và cắt đều ba đường thẳng của tam giác. Nó là một trung tâm của tam giác và là giao điểm của hai trung tâm của hai cạnh của tam giác. Tâm đường tròn nội tiếp được sử dụng trong nhiều lĩnh vực, bao gồm toán học, thiết kế, xây dựng, và các lĩnh vực liên quan. Nó có thể được xác định bằng các công thức toán học hoặc bằng cách sử dụng các phép đo vẽ

Tâm đường tròn nội tiếp tam giác vuông

Với tam giác vuông ABC và tâm đường tròn nội tiếp là O, chúng ta có thể biết:

1. Tâm đường tròn nội tiếp O là giữa hai đường thẳng song song với hai cạnh vuông của tam giác ABC.
2. Các đoạn thẳng BO, CO, và AO là cắt đều ba cạnh của tam giác ABC.
3. AB, BC, và AC là đỉnh của tam giác ABC và là cạnh của tam giác. AB và AC là cạnh vuông của tam giác ABC.
4. Đoạn thẳng OA, OB, và OC là trung tâm của các cạnh của tam giác.
5. Khi AO gặp BO, O là trung điểm của AB.
6. Khi BO gặp CO, O là trung điểm của BC.
7. Khi CO gặp AO, O là trung điểm của AC.
8. Đoạn thẳng BO, CO, và AO đều là trung tâm của các đường tròn nội tiếp của các cạnh vuông của tam giác.

Ví dụ về tâm đường tròn nội tiếp tam giác vuông

Ví dụ: Giả sử tam giác vuông ABC có cạnh vuông cạnh AC và tâm đường tròn nội tiếp là O. Chúng ta muốn tìm độ dài của AO.

Cách giải: Do tam giác vuông ABC, chúng ta có thể biết rằng AO là trung điểm của AC. Do đó, độ dài AO bằng độ dài AC chia 2.

AC = √(AB^2 + BC^2) = √(a^2 + b^2)

Vậy, AO = AC/2 = √((a^2 + b^2)/4).

Đây là một ví dụ cụ thể về cách sử dụng tâm đường tròn nội tiếp tam giác vuông để tìm độ dài của một đoạn thẳng trong tam giác.

Chứng minh tâm đường tròn nội tiếp tam giác

Cách chứng minh rằng tâm đường tròn nội tiếp của tam giác là một điểm trung tâm của tam giác:

1. Tạo hai đường thẳng đối xứng từ các đỉnh của tam giác đến đường tròn nội tiếp.
2. Chứng minh rằng hai đường thẳng này bằng nhau.
3. Chứng minh rằng hai đường thẳng này tạo góc với nhau bằng 120 độ.
4. Chứng minh rằng hai đường thẳng này là đường thẳng song song với đường tròn nội tiếp.
5. Chứng minh rằng tâm đường tròn nội tiếp là trung điểm của hai đường thẳng đối xứng.

Khi chứng minh xong các bước trên, chúng ta có thể chứng minh rằng tâm đường tròn nội tiếp là một điểm trung tâm của tam giác.

Ví dụ về chứng minh tâm đường tròn nội tiếp tam giác

Chứng minh rằng tâm đường tròn nội tiếp của tam giác ABC là điểm I:

1. Tạo hai đường thẳng đối xứng từ các đỉnh của tam giác đến đường tròn nội tiếp.
2. Chứng minh rằng đoạn AB đối xứng từ điểm A đến đường tròn nội tiếp cắt đường tròn nội tiếp tại điểm I, và đoạn BC đối xứng từ điểm B đến đường tròn nội tiếp cắt đường tròn nội tiếp tại điểm I.
3. Chứng minh rằng góc ABI bằng 120 độ bằng cách sử dụng các đạo hàm.
4. Chứng minh rằng AB và BC song song với đường tròn nội tiếp bằng cách sử dụng các đạo hàm.
5. Chứng minh rằng I là trung điểm của AB và BC bằng cách sử dụng các đạo hàm.

Khi chứng minh xong các bước trên, chúng ta có thể chứng minh rằng tâm đường tròn nội tiếp của tam giác là điểm I.

Tâm đường tròn nội tiếp tam giác đều

Tâm đường tròn nội tiếp của tam giác đều là một điểm trong tam giác mà các đường thẳng từ các đỉnh của tam giác đến tâm đường tròn nội tiếp đều song song với các cạnh của tam giác. Tâm đường tròn nội tiếp này còn được gọi là “tâm cân xứng” hoặc “tâm đều”. Nó là một trừu tượng quan trọng trong toán học hình học và được sử dụng rộng rãi trong các ứng dụng của khoa học, công nghệ và xã hội.

Ví dụ về tâm đường tròn nội tiếp tam giác đều

Ví dụ về tâm đường tròn nội tiếp tam giác đều có thể là tam giác ABC có độ dài các cạnh lần lượt là a, b, và c. Tâm đường tròn nội tiếp của tam giác này là điểm O. Các đường thẳng từ đỉnh A, B, và C đến điểm O đều song song với các cạnh của tam giác. Nó cũng có thể chứng minh rằng các đường thẳng từ các đỉnh của tam giác đến điểm O đều có cùng độ dài, bằng nửa chu vi của tam giác.

Tính chất tâm đường tròn nội tiếp tam giác

Có nhiều tính chất của tâm đường tròn nội tiếp tam giác mà ta có thể trình bày với các từ vựng chuyên sâu hoặc dễ hiểu hơn:

1. Tọa độ: Tâm đường tròn nội tiếp của tam giác là một điểm cụ thể trong tam giác, vì vậy nó có thể được biểu diễn bằng tọa độ.
2. Độ dài: Các đường thẳng từ các đỉnh của tam giác đến tâm đường tròn nội tiếp đều có cùng độ dài, bằng nửa chu vi của tam giác.
3. Tính song song: Các đường thẳng từ các đỉnh của tam giác đến tâm đường tròn nội tiếp đều song song với các cạnh của tam giác.
4. Tính chất cân xứng: Tâm đường tròn nội tiếp là tâm của tam giác, vì vậy nó cân xứng các đoạn đường giữa các đỉnh và tâm đường tròn nội tiếp.
5. Ứng dụng: Tâm đường tròn nội tiếp tam giác đều là một trừu tượng quan trọng trong toán học hình học và được sử dụng rộng rãi trong các ứng dụng của

Trong chương trình Toán lớp 9 các em sẽ làm quen với đường tròn nội tiếp, ngoại tiếp của tam giác. Kiến thức trong sách khóa khoa đã đầy đủ tuy nhiên chúng tôi sẽ bổ sung và tóm tắt các ý chính của phần này và phương pháp giúp xác định tâm đường tròn nội tiếp, ngoại tiếp của tam giác. Mời học sinh cùng theo dõi để hiểu rõ hơn bài học ngày hôm nay.

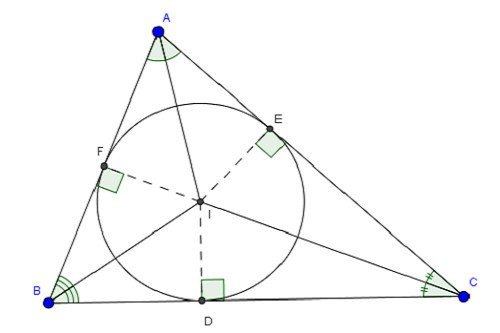
Đường tròn nội tiếp tam giác là gì?

Đường tròn nội tiếp tam giác là khái niệm mà nhiều học sinh quan tâm. Đường tròn nội tiếp tam giác xảy ra khi 3 cạnh của tam giác là tiếp tuyến của đường tròn và đường tròn này sẽ nằm trong tam giác đó.

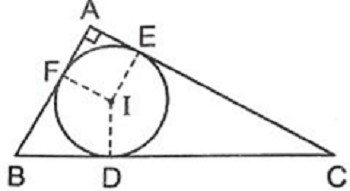
Đường tròn ngoại tiếp tam giác là gì?

Đường tròn ngoại tiếp tam giác là đường tròn sẽ đi qua cả 3 đỉnh của một tam giác. Hay nhiều người thường gọi theo cách khác là tam giác nội tiếp đường tròn.

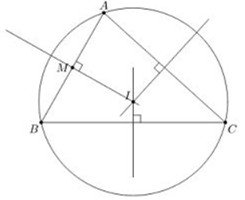
Khi làm quen với đường tròn nội tiếp và ngoại tiếp của tam giác học sinh sẽ tìm hiểu thêm về khái niệm đường trung trực. Đường trung trực sẽ được định nghĩa như sau: đườn trung trực đoạn thẳng AB là đường thẳng đi qua trung điểm M của AB và vuông góc với AB. Mọi điểm I nằm trên trung trực của AB đều sẽ là IA=IB.

Cách xác định tâm đường tròn nội tiếp, ngoại tiếp tam giác

Muốn xác định tâm đường tròn nội tiếp của tam giác và tâm đường tròn ngoại tiếp tam giác học sinh cần lưu ý phần đã nêu trong lý thuyết:

– Tâm đường tròn nội tiếp của tam giác là giao điểm của ba đường phân giác bên trong của tam giác (cũng có thể là giao điểm 2 đường phân giác)

– Tâm đường tròn ngoại tiếp tam giác là vị trí giao điểm của ba đường trung trực đó là ba cạnh tam giác (cũng có thể là giao điểm 2 đường trung trực).

Phương pháp giải bài tập đường tròn nội tiếp tam giác

Bài tập đường tròn nội tiếp và ngoại tiếp tam giác có một số dạng như sau, các em học sinh theo dõi để nắm chắc các dạng toán và từ đó tìm ra phương pháp giải các dạng trên.

Dạng 1: Tìm tâm đường tròn nội tiếp tam giác khi đã có thông tin tọa độ ba đỉnh.

Ví dụ: Mặt phẳng Oxy có tam giác ABC với A(1;5) B(–4;–5) và C(4;-1). Đi tìm tâm I đường tròn nội tiếp tam giác ABC.

Dạng 2: Tìm bán kính đường tròn nội tiếp tam giác

Ví dụ: Mặt phẳng Oxy cho tam giác ABC với A(2;6), B(-3;-4), C(5;0). Học sinh xác định bán kính đường tròn ngoại tiếp của tam giác ABC

Dạng 3: Viết phương trình đường tròn nội tiếp tam giác ABC với thông tin đã cho đó là tọa độ 3 đỉnh.

Ví dụ: Trong mặt phẳng hệ tọa độ Oxy, tam giác ABC có A(11; -7), B(23;9), C(-1,2). Hãy viết phương trình đường tròn nội tiếp của tam giác ABC.

Một số bài tập đề nghị

Bài 1  Trong mặt phẳng Oxy cho tam giác ABC với thông tin A(1;5) B(–4;–5) và C(4;-1).Hãy tìm tâm J của đường tròn nội tiếp tam giác ABC .

Đáp án bài 1:  J(1;0)

Bài 2  Trong mặt phẳng Oxy cho tam giác ABC với các thông tin A(-15/2; 2), B(12; 15), C(0; -3). Hãy đi tìm tâm J của đường tròn nội tiếp tam giác ABC.

Đáp án bài 2:  J(-1;2)

Bài 3 Trong mặt phẳng Oxy cho tam giác ABC với A(3;–1) B(1;5) và C(6;0) . Gọi A’ là chân đường cao kẻ từ A lên BC tìm A’ .

Đáp án bài 3:  A'(5;1)

Đọc thêm: Công thức tính diện tích tam giác: Thường, Vuông, Cân, Đều

Vừa rồi là khái niệm về đường tròn nội tiếp và ngoại tiếp của tam giác, cách tìm tâm đường tròn nội tiếp, ngoại tiếp tam giác. Phương pháp giải bài tập đường tròn nội tiếp tam giác mà học sinh lớp 9 cần nhớ. Đây là dạng bài tập quan trọng trong chương trình Toán học 9. Nắm chắc kiến thức và thực hành các dạng bài tập sẽ giúp có kết quả cao trong các bài kiểm tra, thi cuối kì.

Chúc các em học tốt.

Bài Liên Quan: