Tính khoảng cách giữa 2 đường thẳng là khái niệm toán học xuất hiện trong chương trình Toán học cấp 2 và cấp 3. Giải thích 2 đường thẳng chéo nhau là gì? Làm thế nào để tính khoảng cách giữa 2 đường thẳng chéo nhau? Mời các bạn học sinh theo dõi phần lý thuyết ngay bên dưới. Chắc chắn sẽ quan trọng và cần thiết khi học tại lớp.
Contents
Đường thẳng là gì?
Đường thẳng giải nghĩa là một đường dài, mỏng và thẳng tuyệt đối. Hình học Euclide, chỉ có một đường thẳng đi qua hai điểm bất kỳ khác nhau. Đường thẳng này chính là đoạn nối ngắn nhất giữa hai điểm.
Hai đường thẳng chéo nhau là gì?
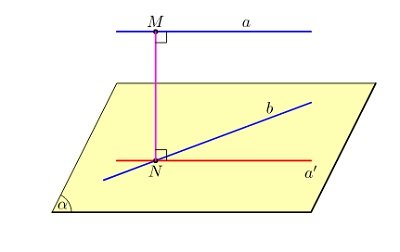
Hai đường thẳng chéo nhau được định nghĩa đơn giản như sau: Hai đường thẳng chéo nhau trong không gian trong trường hợp chúng không cùng một mặt phẳng, không song song và cũng không cắt nhau.
Cách tính khoảng cách giữa 2 đường thẳng chéo nhau
Chúng ta có thể tính khoảng cách giữa hai đường thẳng chéo nhau d1; d2, bằng các cách như sau:
Cách 1: Xác định đường vuông góc chung
Khi đề bài có thông tin hai đường thẳng d1; d2 vuông góc với nhau . Chúng ta thực hiện như sau:
Bước 1 : Xác định 1 mặt phẳng (P) chứa đường thẳng d1 vuông góc với đường thẳng d2. Có nghĩa là đường thẳng d2 vuông góc với hai đường thẳng cắt nhau nằm trong cùng mặt phẳng (P) , bao gồm có đường thẳng d1.
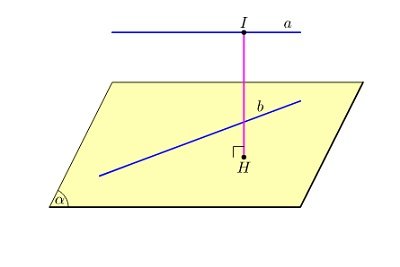
Bước 2 : Tìm giao điểm I đường thẳng d2 với mặt phẳng (P) . Từ I kẻ IH vuông góc với d1, với H ∈ d1. Khi đó IH là đoạn vuông góc chung hai đường thẳng d1; d2.
Bước 3 : Xác định độ dài đoạn thẳng IH .
Áp dụng hệ thức lượng tam giác và tam giác đồng dạng, định lý Pitago xác định độ dài của đoạn thẳng IH.
Cách 2: Dựa vào khoảng cách của đường thẳng và mặt phẳng song song.
Bước 1 : Lấy mặt phẳng (P) sẽ có chứa đường thẳng d, song song với đường thẳng d . Khi đó thì
d(d1, d2) = d(d2, (P)).
Chúng ta nên lấy để dễ dàng tính được khoảng cách .
Bước 2 : Xác định khoảng cách giữa đường thẳng d với mặt phẳng (P).
Cách dựng đoạn vuông góc chung hai đường thẳng chéo nhau a và b
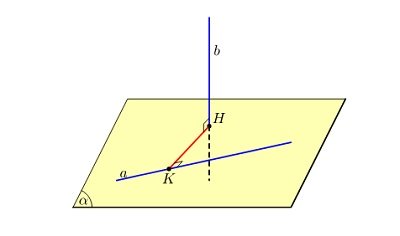
Dựng mặt phẳng () có chứa thoả sao cho () song song với ,
Tìm hình chiếu vuông góc ′ của trên (),
Xác định giao điểm của ′ và , dựng đường thẳng Δ đi qua , vuông góc với () cắt tại điểm . Đoạn đoạn vuông góc chung của và .
Tính khoảng cách giữa hai đường thẳng chéo nhau (trường hợp đặc biệt)
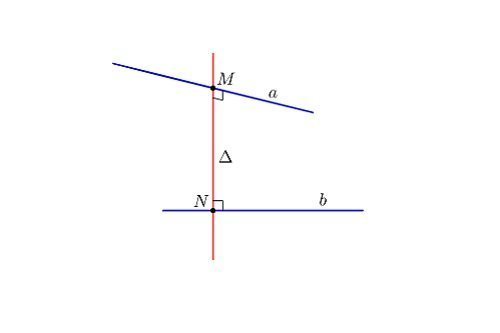
Xác định khoảng cách giữa 2 đường thẳng chéo nhau đặc biệt và chéo nhau và vuông góc với nhau, tồn tại một mặt phẳng () chứa và vuông góc với . Xác định khoảng cách giữa và ta dựng đoạn vuông góc chung:
Xác định giao điểm của và (),
Trong (), hãy vẽ vuông góc với tại điểm . Lúc này chính là đoạn vuông góc chung.
Bài tập thực hành
Bài 1: Cho tứ diện ABCD có AB=x , CD=b, mỗi cạnh còn lại đều bằng a. Ta gọi EF là trung điểm của AB và CD.
a) Chứng minh AB vuông góc với CD và EF đường vuông góc chung AB và CD. Hãy tính EF theo a,b, x.
b) Tìm ra cho 2 mặt phẳng ACD và BCD vuông góc.
Bài 2: Cho hình lập phương ABCD A’B’C’D’ với cạnh a.
a) Tính theo a để khoảng cách 2 đường thẳng A’B và DB’.
b) Gọi M N P là các trung điểm của BB’, Cd, A’D’. Hãy tính góc của hai đường thẳng MP và đoạn thẳng C’N.
Bài 3: Ta có lăng trụ đứng ABC.A’B’C’ có các cạnh đều là a. Với M là trung điểm AA’. Hãy chứng minh BM vuông góc với B’C. Xác định khoảng cách của BM và B’C.
Xem thêm: Thế nào là 2 góc phụ nhau
Các bạn vừa theo dõi hướng dẫn cách tính khoảng cách giữa 2 đường thẳng chéo nhau. Đây là kiến thức cơ bản trong chương trình toán học trung học và phổ thông. Ghi nhớ lý thuyết và thực hành tốt trong các bài tập tại lớp hoặc thi cử.
Chúc các bạn học tốt!